Mathematics behind rotation Part 1

This will be a tutorial series on rotating sprites and 3D models. The first part will take you through the mindset of rotation and explain in theory how rotations work. The second part is the more mathematical part about rotation using matrices and applying this for 3D rotations.

This short part of the tutorial will be on rotating sprites. First I will explain about rotation in general, define ‘good’ and ‘bad’ rotations, and after that I will continue by pointing out how we can define this in the ‘digital world’ as I will call it from now on.

Lets start with the basics behind rotation in 2D. Say you have a nice image you wish to rotate shown here as the green square. If you want to rotate it by 45 degrees, you will want to expect the yellow square here. For some of you this will be perfectly normal, and it should be. However, usually when you rotate an image in your code and look at what happens, we see the red squares appear when rotating 90 or 225 degrees. How does this happen, and more importantly how do we fix this?



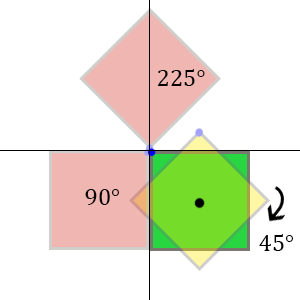
Going back to the digital world, we have some other sense of logic. It will all make complete sense in a moment but bear with me. An image is usually represented as a 2 dimensional array of information, starting at [0,0] and ending at [X,Y] with X as width and Y as height of your image. So the least you know about your image is it starts at [0, 0], right? Thats exactly why this ‘bad’ rotation from green to the red squares happens. I marked the top left corner of the image with a blue dot, this is the position [0,0] of your image. As you'll see this blue dot will stay pretty much on the axis I’ve drawn. So, if you would just say to your compiler:
"rotate my image 90 degrees!" Your compiler would just say: "okay, I will rotate it around the origin for you, you have not specified anything so I will assume your origin is centered at [0, 0]!" Hence the result shown in the image above shows up.

So how do we fix this? We want to get the result shown as the yellow square above. To realise this we have to rotate the image around its own axis. Shown in the image is the center of the green square with a black dot. What we want to do here is set the axis for the rotation on this point. So basically you just put a hinge in the center of the square and rotate it around that. Now to represent this in the digital world, lets go back to the origin of your image: [0, 0]. We want this origin to be the center of the green square.



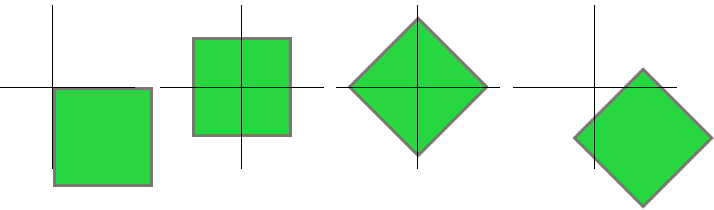
For the complete rotation to work you will have to move the square so that the center of the image is positioned at the axis, shown here in the image above. Once you have done this you can rotate your image freely without consequences. At the end don’t forget to return it to its original position!

This was it for part 1 of this tutorial. In the next part we will continue on doing this correct rotation by using matrices and then applying it on 3D models.

Continue to part 2